Oblique Hip Guide
By Domenico Mazza
This guide will walk you through on how to calculate angles and lengths for an oblique hip roof. The guide is a work in progress for the development of oblique hip calculation at hip roof calculator. 
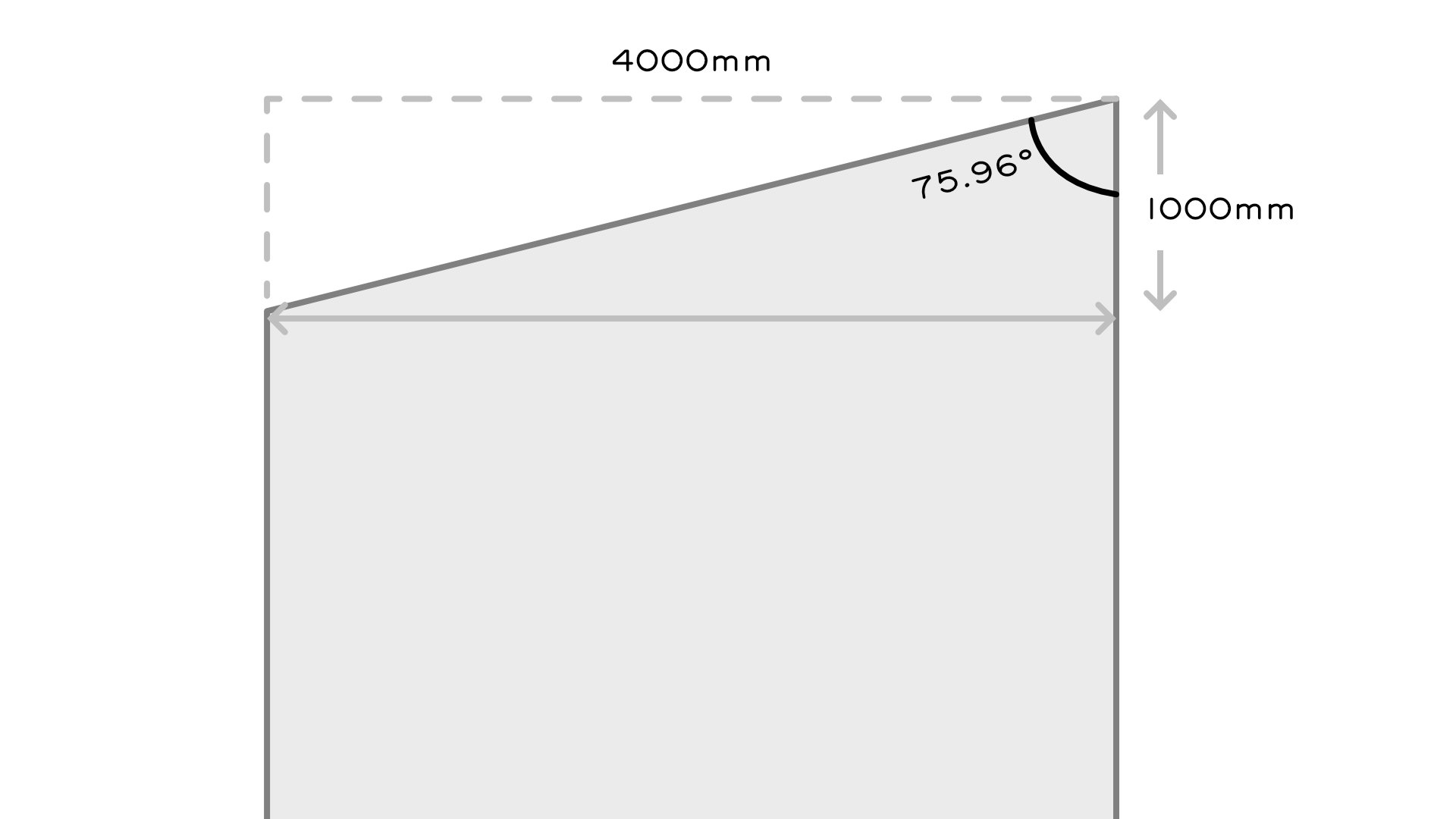
- The oblique hip roof has a Width and Offset. In our example here:
- Width is 4000mm
- Offset is 1000mm
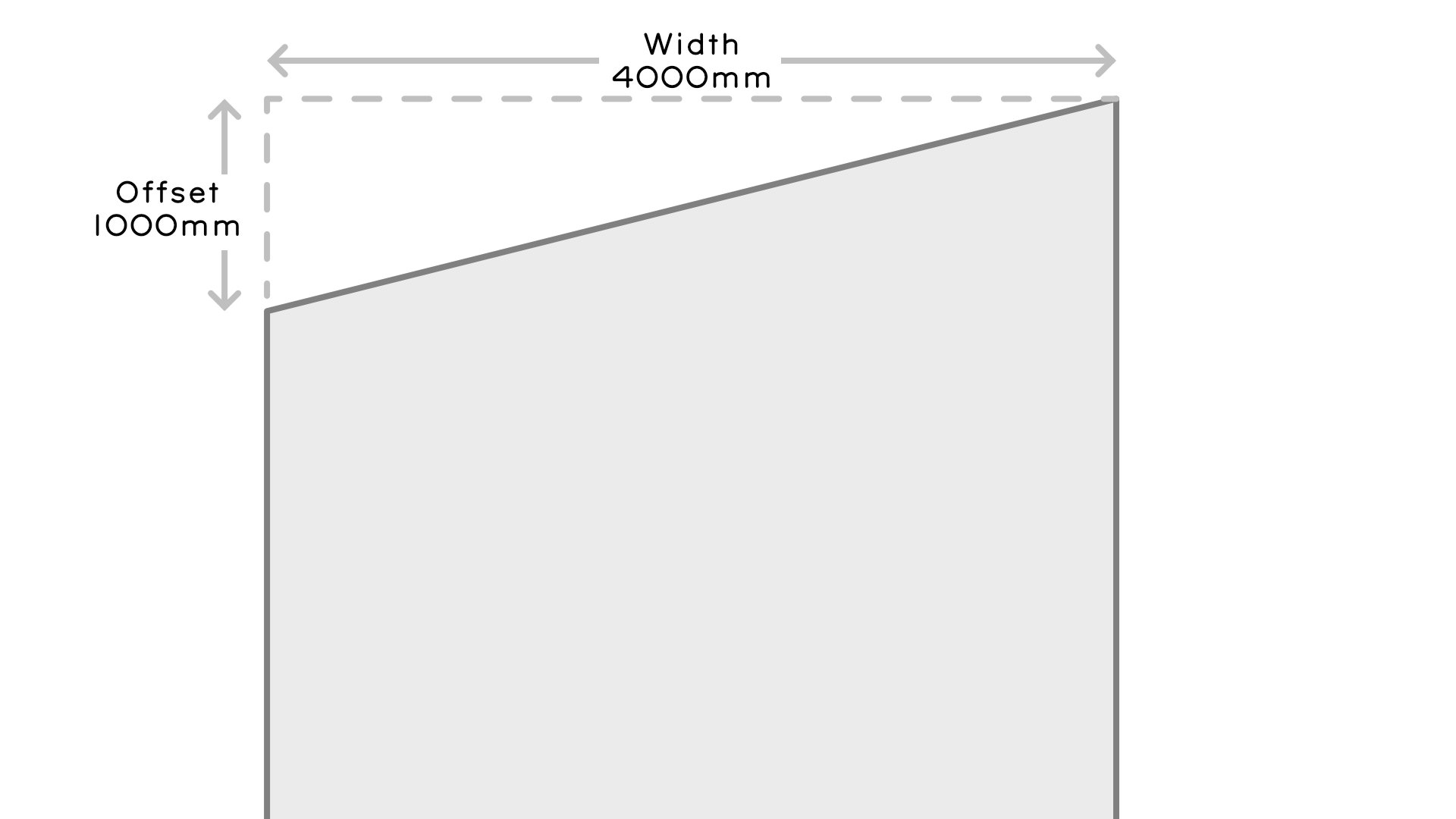
- If we imagine a right angle triangle created by the width and offset, the hypotenuse distance is the Oblique End. We use the formula a2 + b2 = c2, to solve for c: √(1000×1000 + 4000×4000) = 4123mm for our Oblique End length
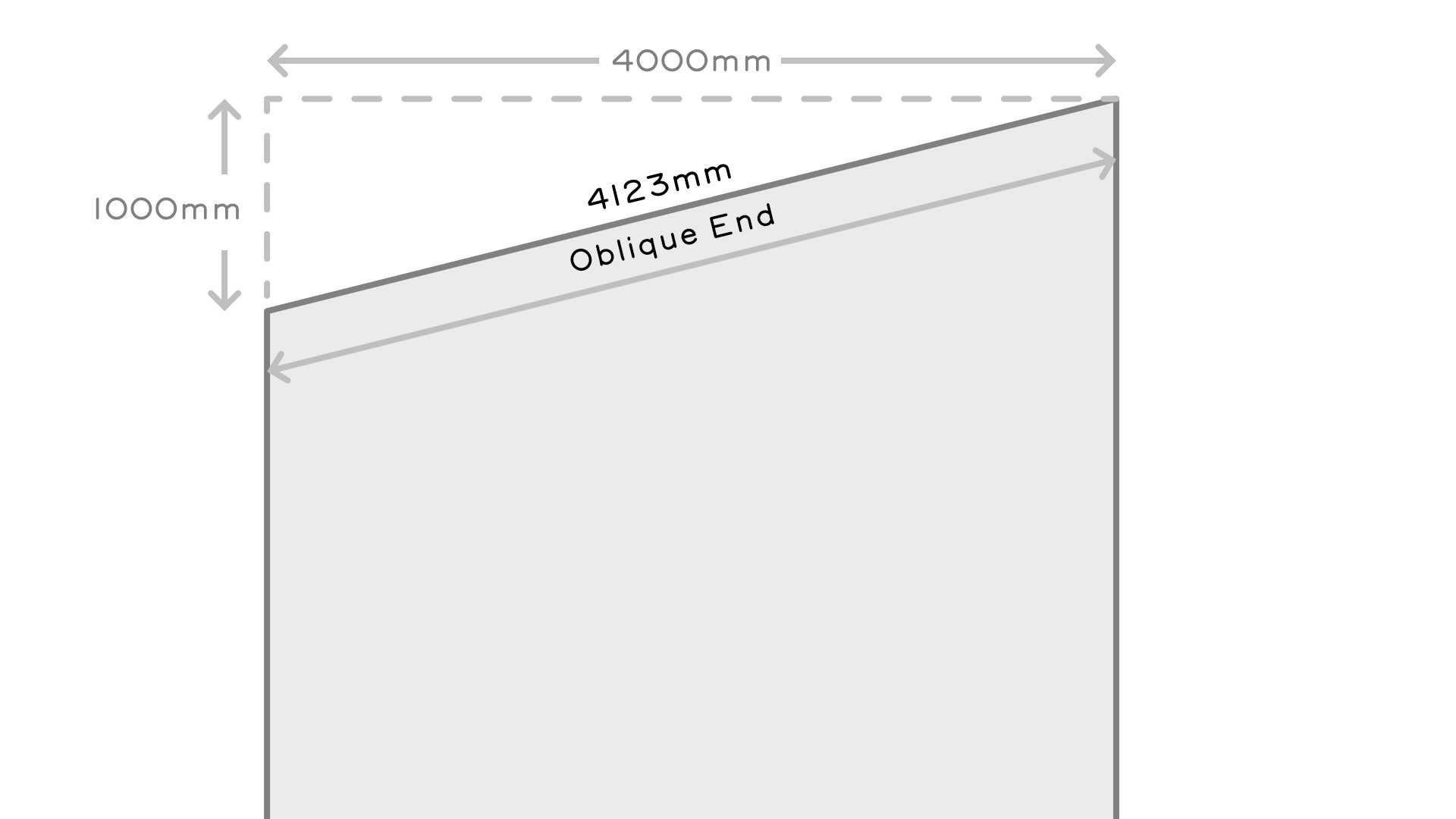
- If we draw a line from the middle of the Oblique End, which is half the length of the Oblique End, it will equal the distance to the Gathering Point on the tip of the Ridgeboard, which is 4123mm / 2 = 2061.5mm
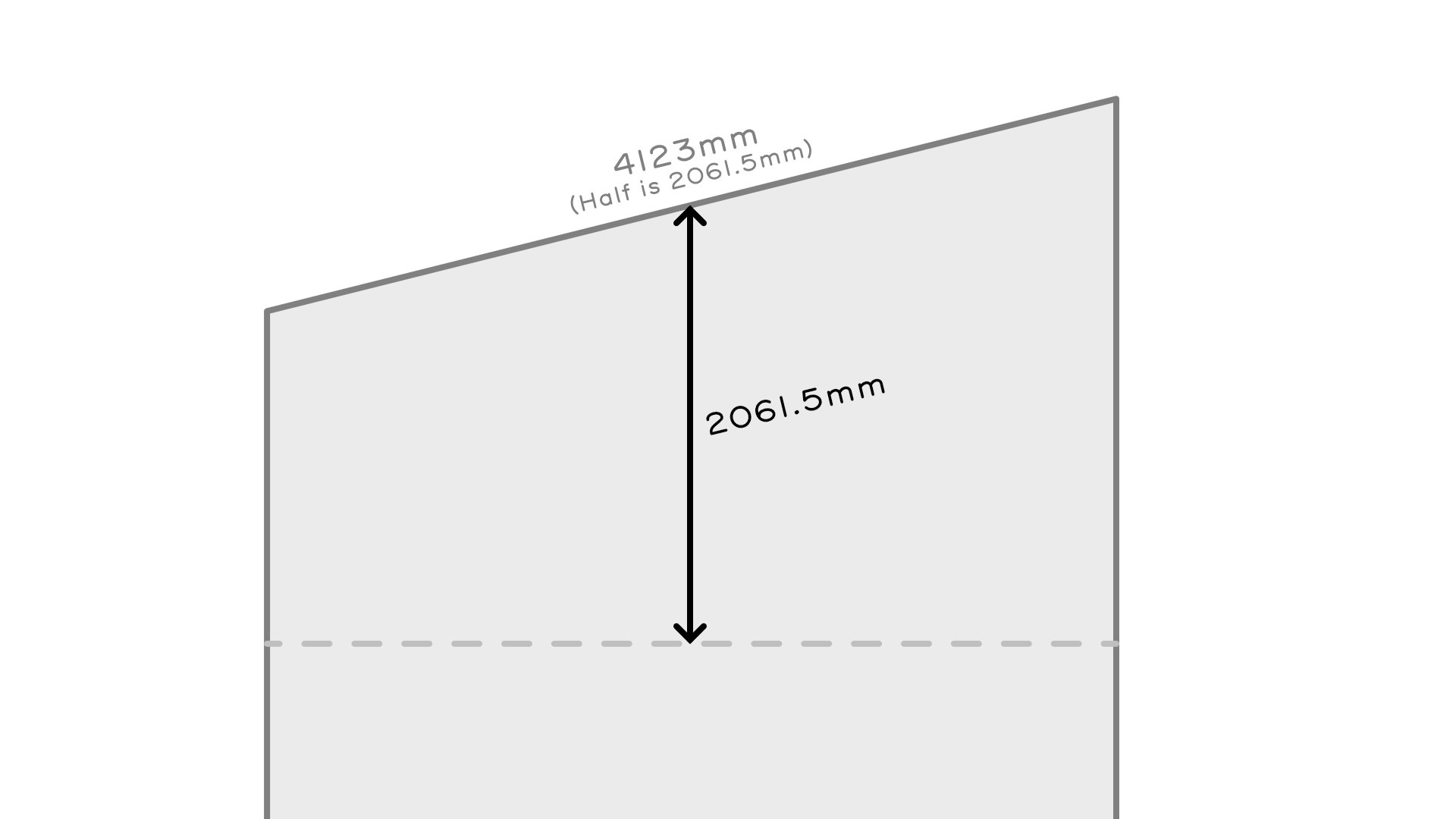
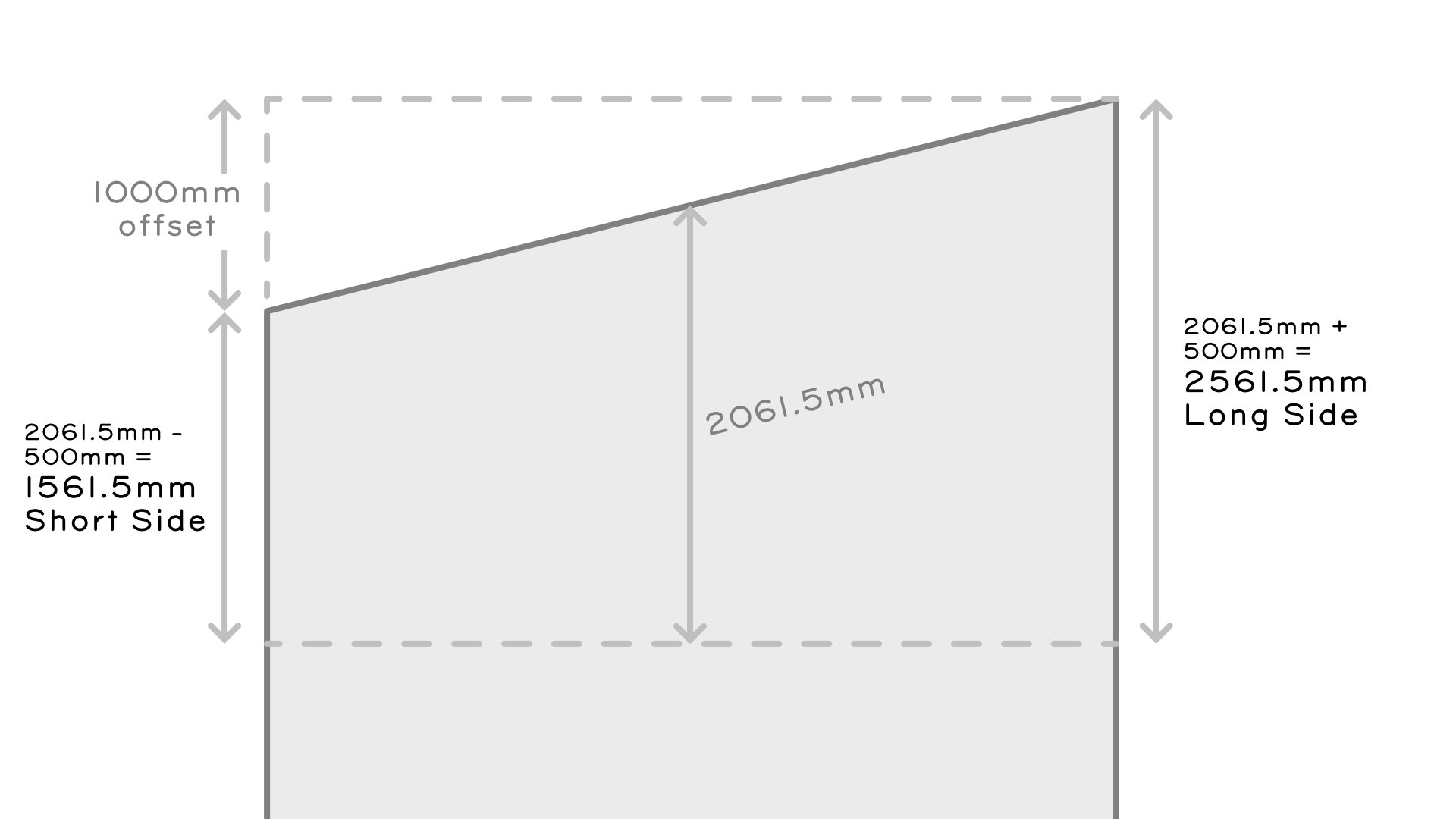
- The Oblique End half length line of 2061.5mm, also happens to sit halfway between the Offset of 1000mm. Our Offset halved is 500mm. These values allows us to calculate our Short Side and Long Side lengths.
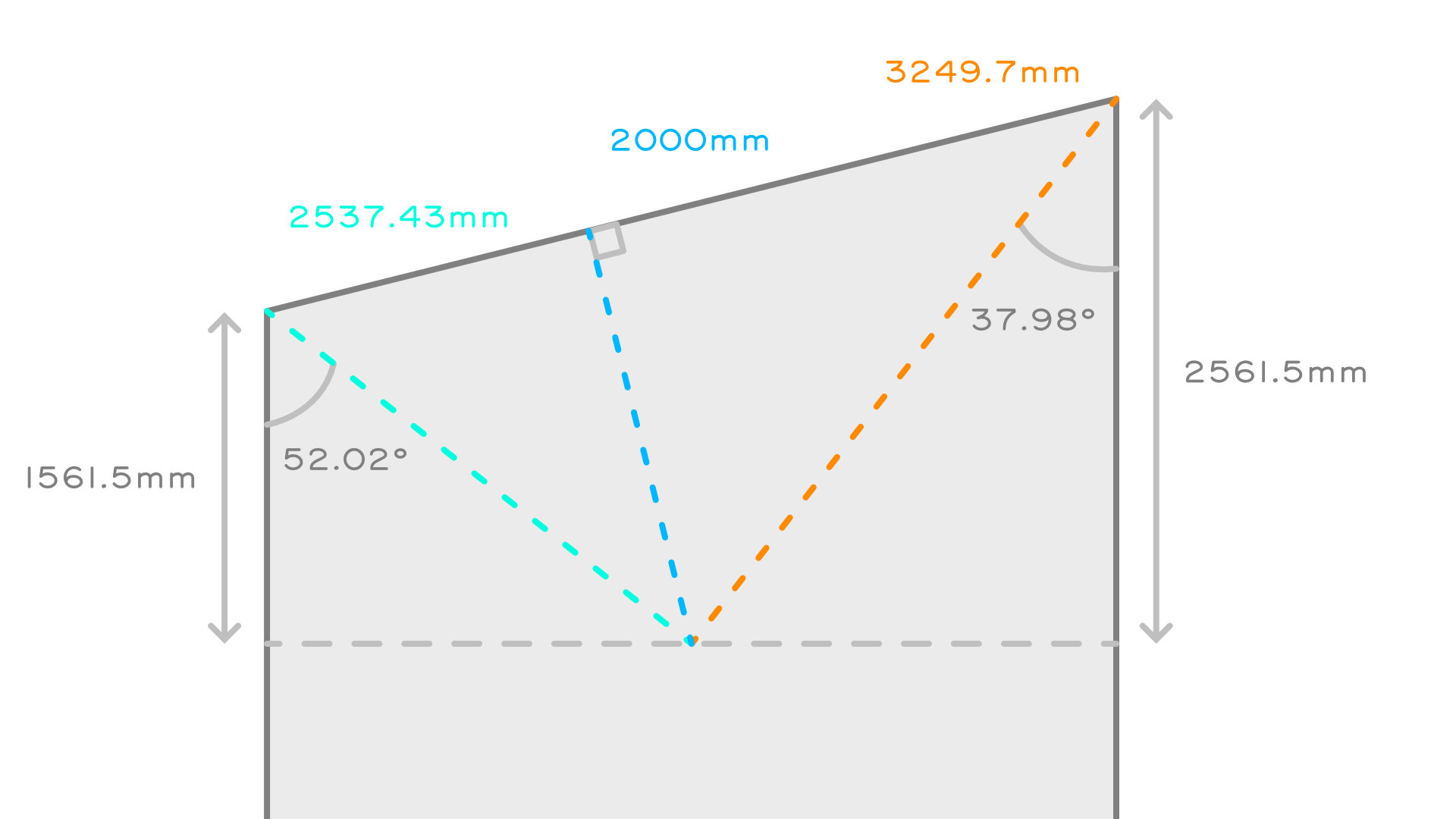
- The Short Side length is: 2061.5mm - 500mm = 1561.5mm
- The Long Side length is: 2061.5mm + 500mm = 2561.5mm
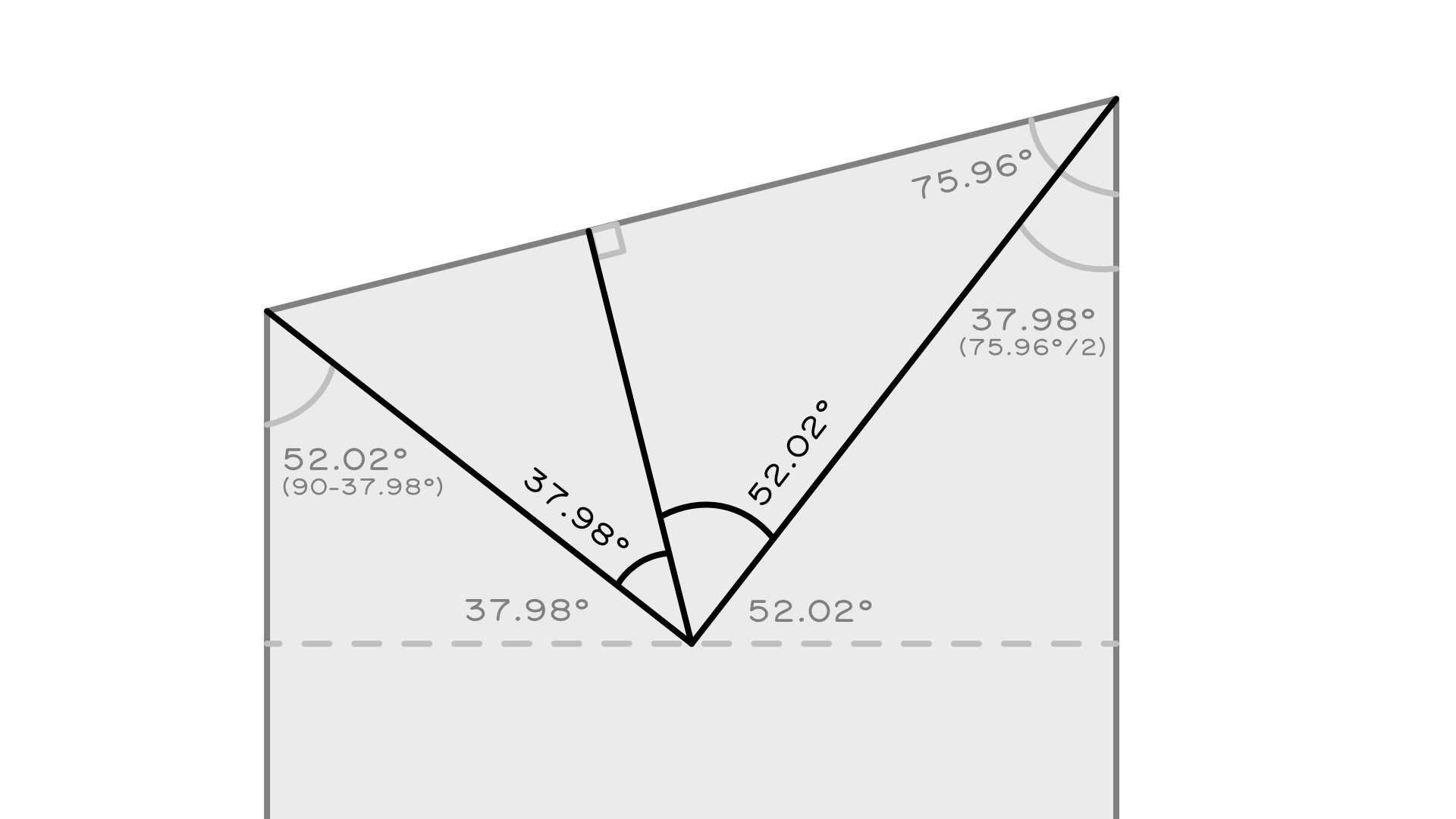
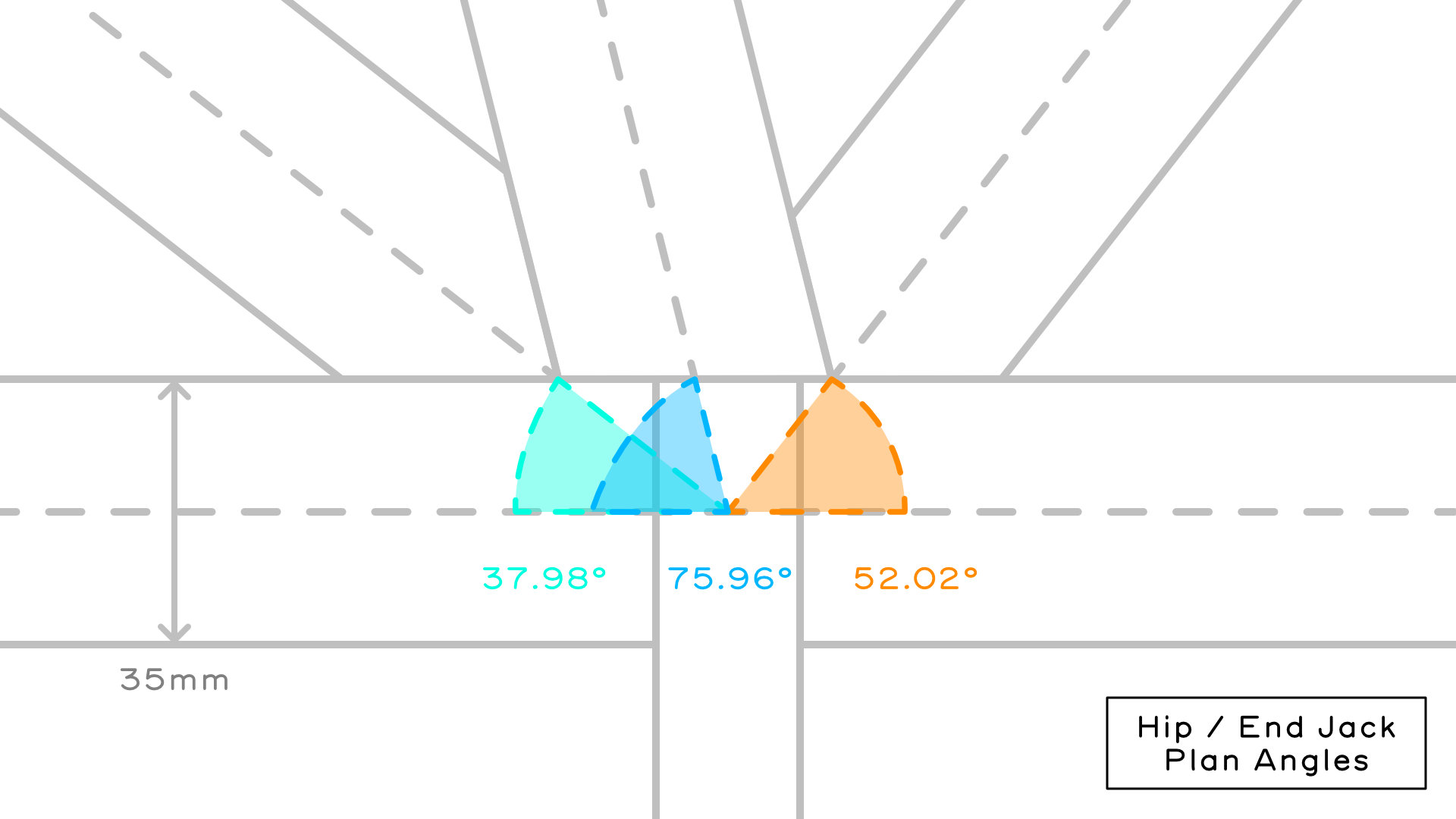
- The angle created by the width and offset on the Long Side provides us with the first step in finding all of our required plan angles. If we use trigonometry, our width 4000mm can be our 'opposite' side and our offset 1000mm the 'adjacent' side. As a rule of thumb we remember SOH CAH TOA, where θ is the adjacent angle: sin(θ) = opposite / hypotenuse, cos(θ) = adjacent / hypotenuse, and tan(θ) = opposite / adjacent. We choose TOA, so tan applies. The tan of the angle is 4000mm / 1000mm. We need to use the inverse of tan (a.k.a. arctan or tan-1) to move it to the other side of the equation and extract the angle. Our angle is arctan(4000/1000) = 75.96°
- Since our Long Side plan angle is 75.96° dividing this in half gives us our Long Side Hip Plan Angle, 75.96° / 2 = 37.98°. We need this later to calculate the pitch of that hip.
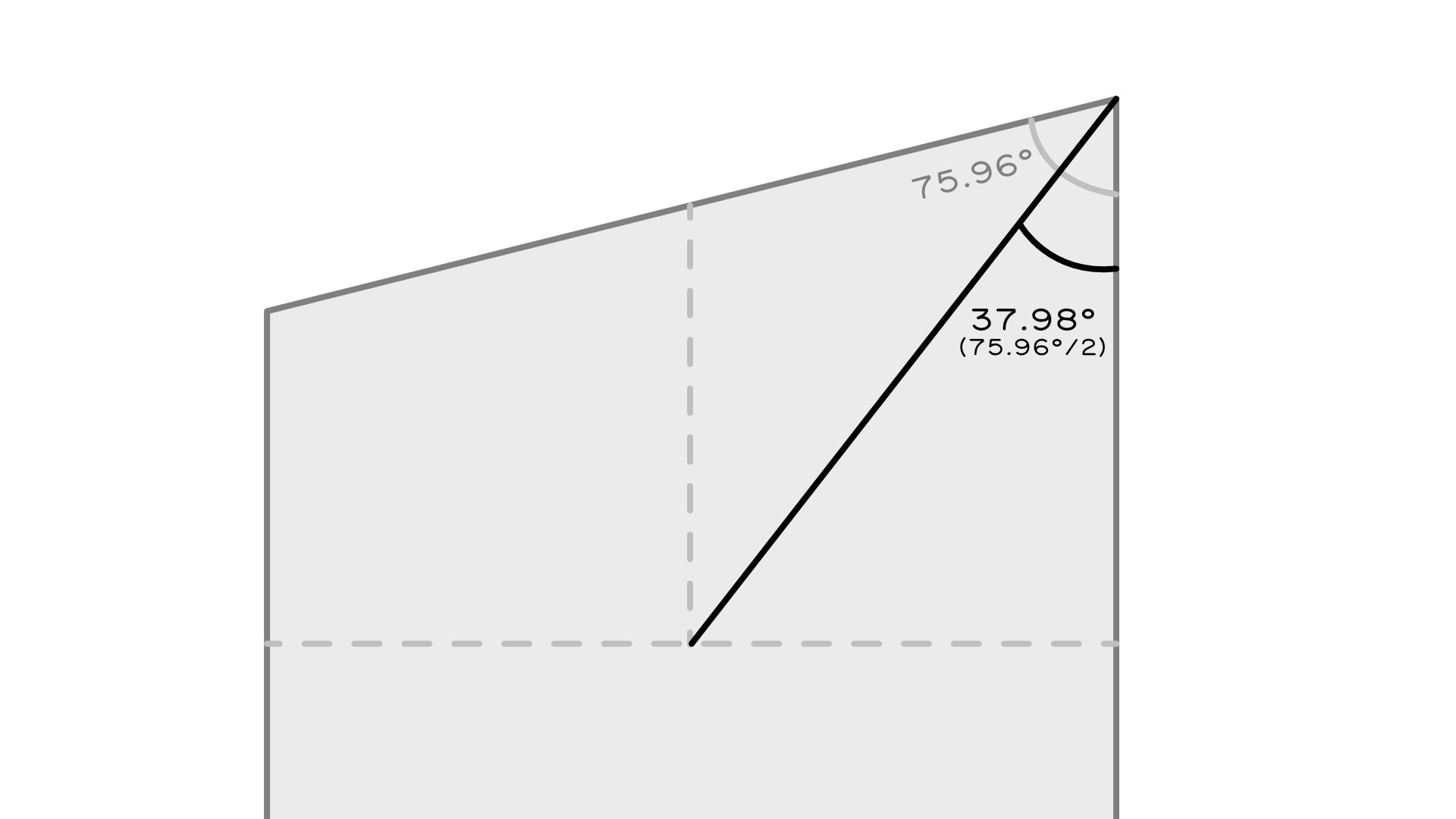
- Because our hips meet at a right angle (90°) at the Gathering Point, we can subtract 37.98° from 90° and find that the Short Side Hip Plan Angle is 52.02°.

- The end jack runs perpendicular at 90° from the oblique hip to the Gathering Point.

- We can now work out the plan lengths for the end jack and hips. Our End Jack Plan Length will be 2000mm given that is the half-span of our 4000mm wide roof. To find the hip plan lengths we can treat them as hypotenuse sides. Our adjacent angles are the Long Side Hip Plan Angle at 37.98° and the Short Side Hip Plan Angle at 52.02°. Our adjacent sides are the Short Side and Long Side lengths. We apply CAH, cos(adjacent angle) = adjacent side length / hypotenuse. Our Long Side hypotenuse = 2561.5 / cos(37.98°) = 3249.7mm, this is our Long Side Hip Plan Length. Our Short Side hypotenuse = 1561.5/cos(52.02) = 2537.43mm, this is our Short Side Hip Plan Length
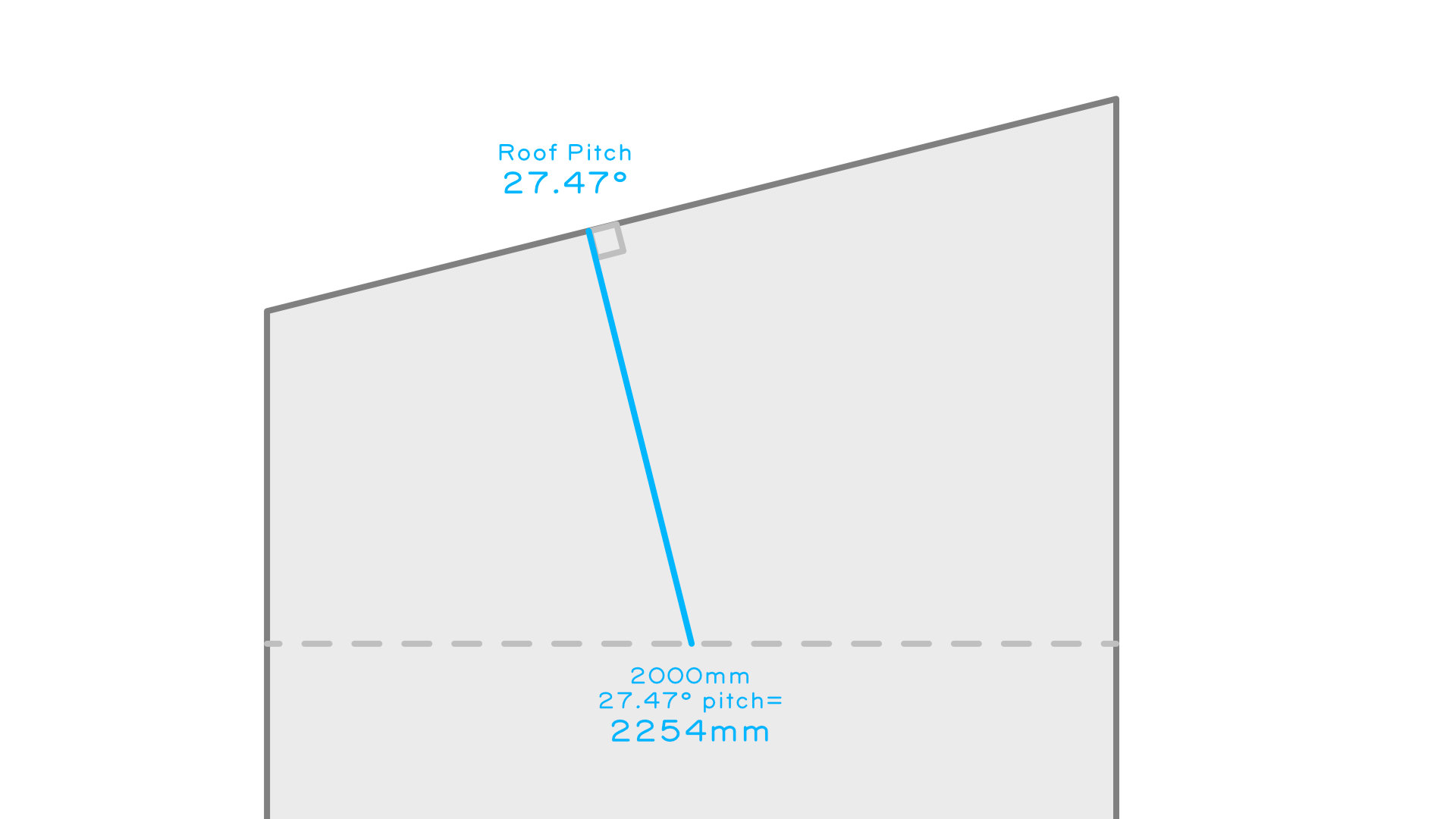
- Now we need to get these lengths off the plan and into the 'air' to get actual lengths. For our end jack we imagine a triangle where the roof pitch is the adjacent angle, our hypotenuse will be the length. Our adjacent length is 2000mm. CAH applies, cos(roof pitch) = 2000mm/hypotenuse, so the End Jack Length is 2000mm/cos(27.47) = 2254mm.
- Now the magic to figure out the hip angles. We can use the formula arctan(tan(roof pitch) × sin(hip plan angle)). Notes are provided below on how this formula works. For now, if we plug in the respective hip plan angles: arctan(tan(27.47°) × sin(37.98°)) gives us 17.74° for the Long Side Hip Angle and arctan(tan(27.47°) × sin(52.02°)) gives us 22.28° for the Short Side Hip Angle
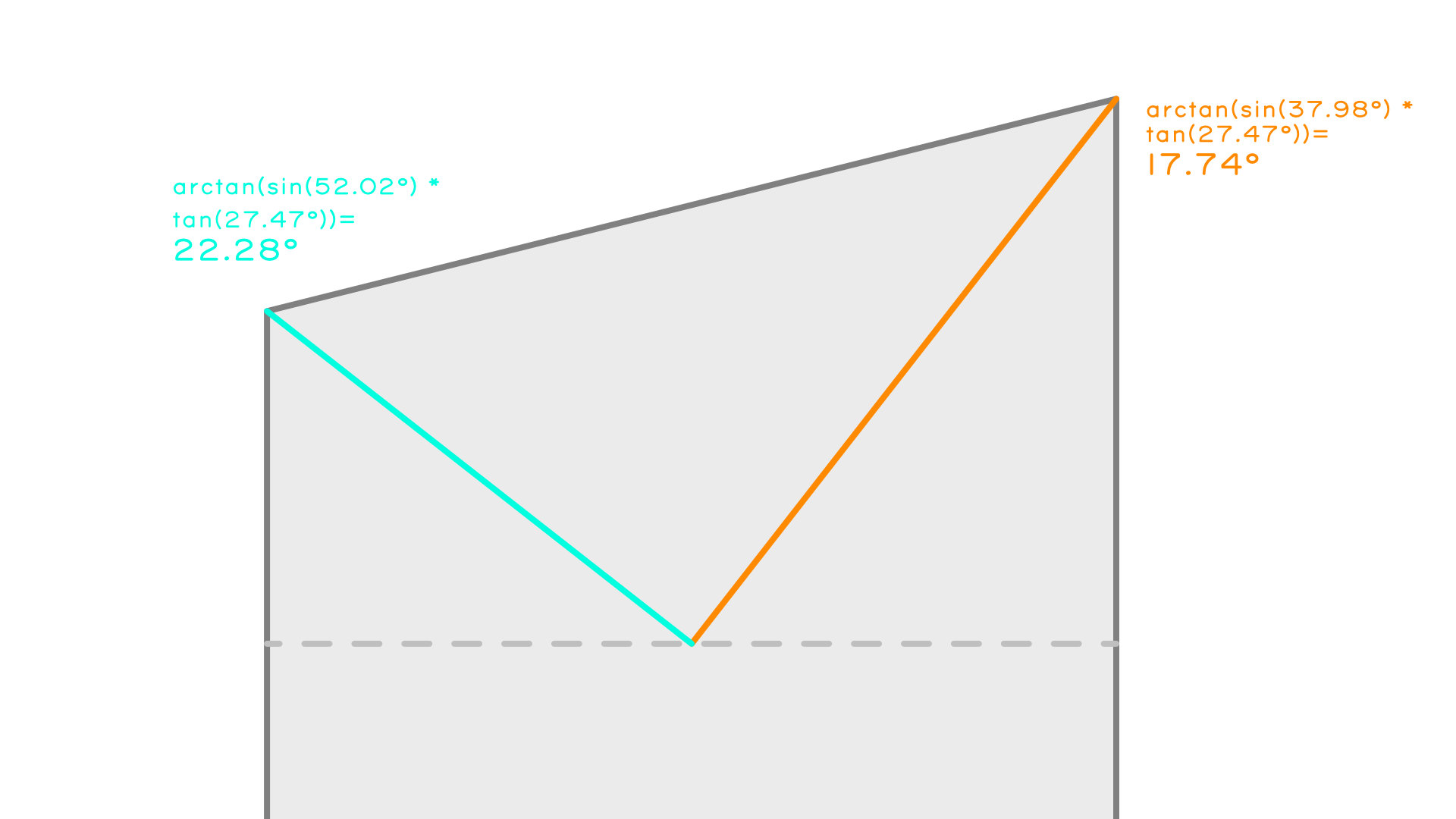
- Now that we have our hip angles we can find the hip lengths, from the plan lengths. We know our Long Side Hip Plan Length is 3249.7mm and our Short Side Hip Plan Length is 2537.43mm. Imagining a triangle where the hypotenuse is the hip length, CAH applies: cos(hip angle) = hip plan length / hip length, the hip length = hip plan length / cos(hip angle). The Long Side Hip Length is 3249.7mm / cos(17.74°) = 3412mm. The Short Side Hip Length is 2537.43mm / cos(22.28°) = 2742mm
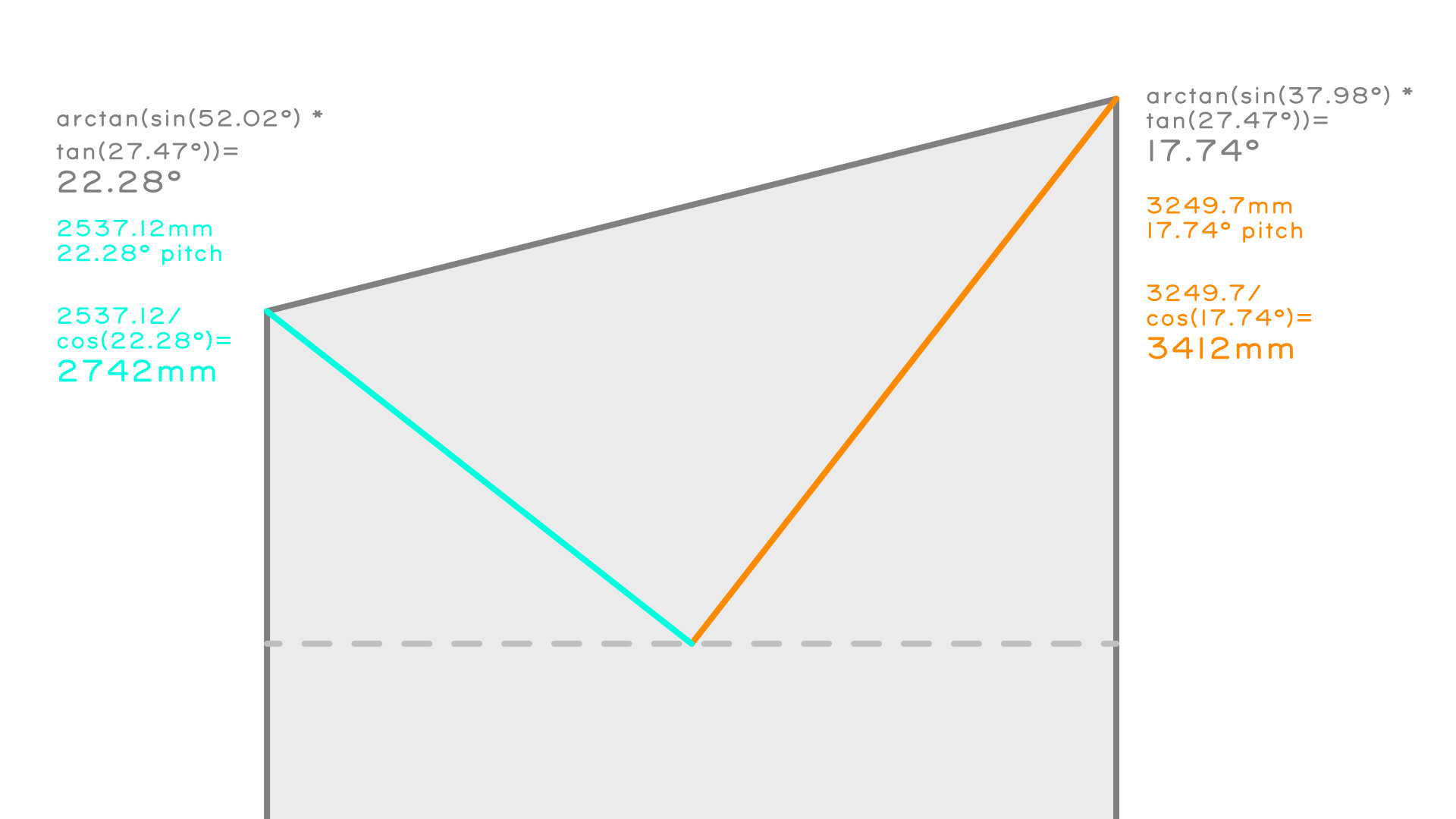
- The hip lengths require side cuts. The side cut angles are the respective hip plan angles minus 90° to get the opposite angle. For the Short Side Hip it's 90° - 52.02° = 37.98°. For the Long Side Hip it's 90° - 37.98° = 52.02°. Set your circular saw or compound mitre saw to the side cut angle and cut along the plumb cut angle.
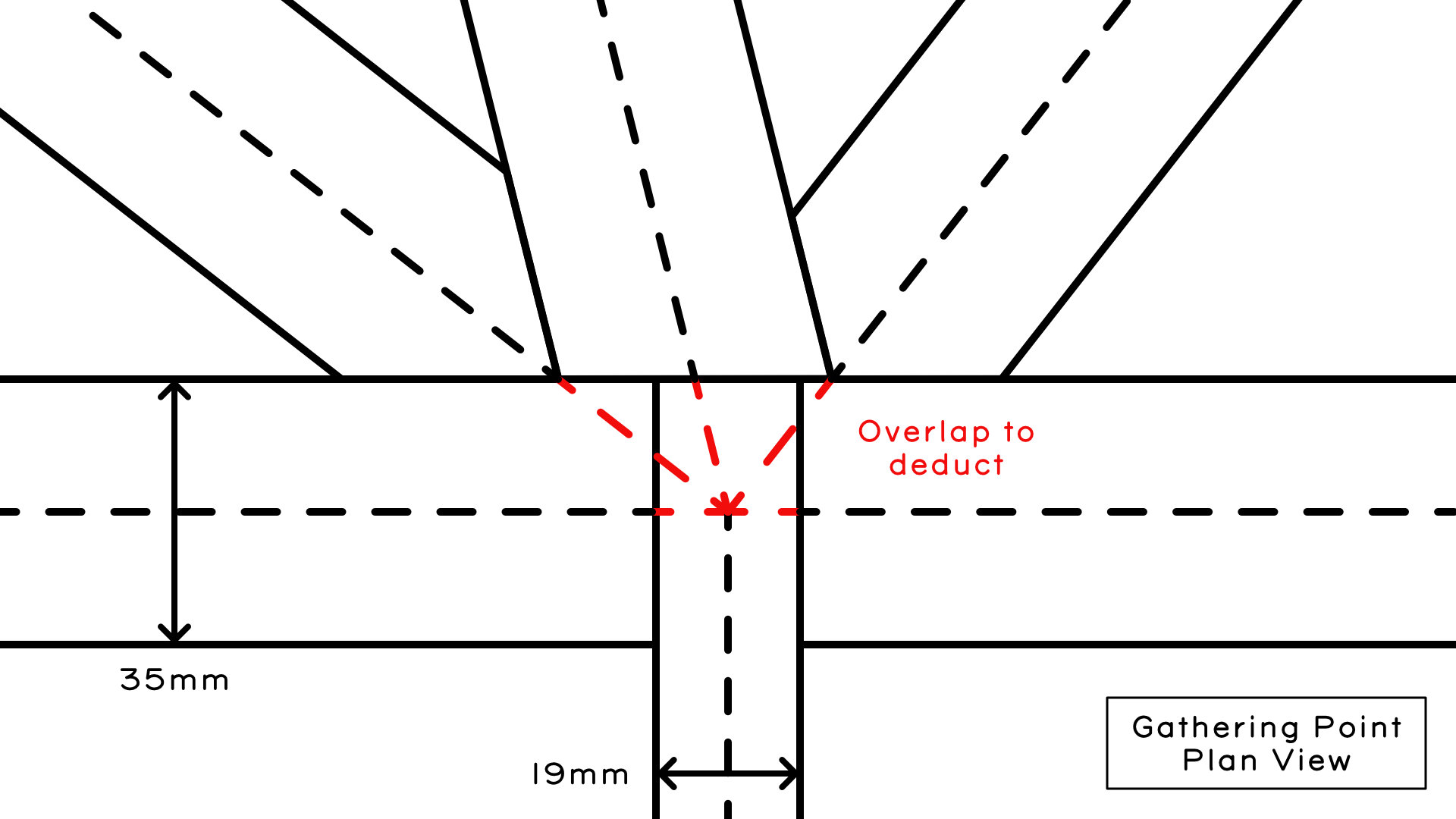
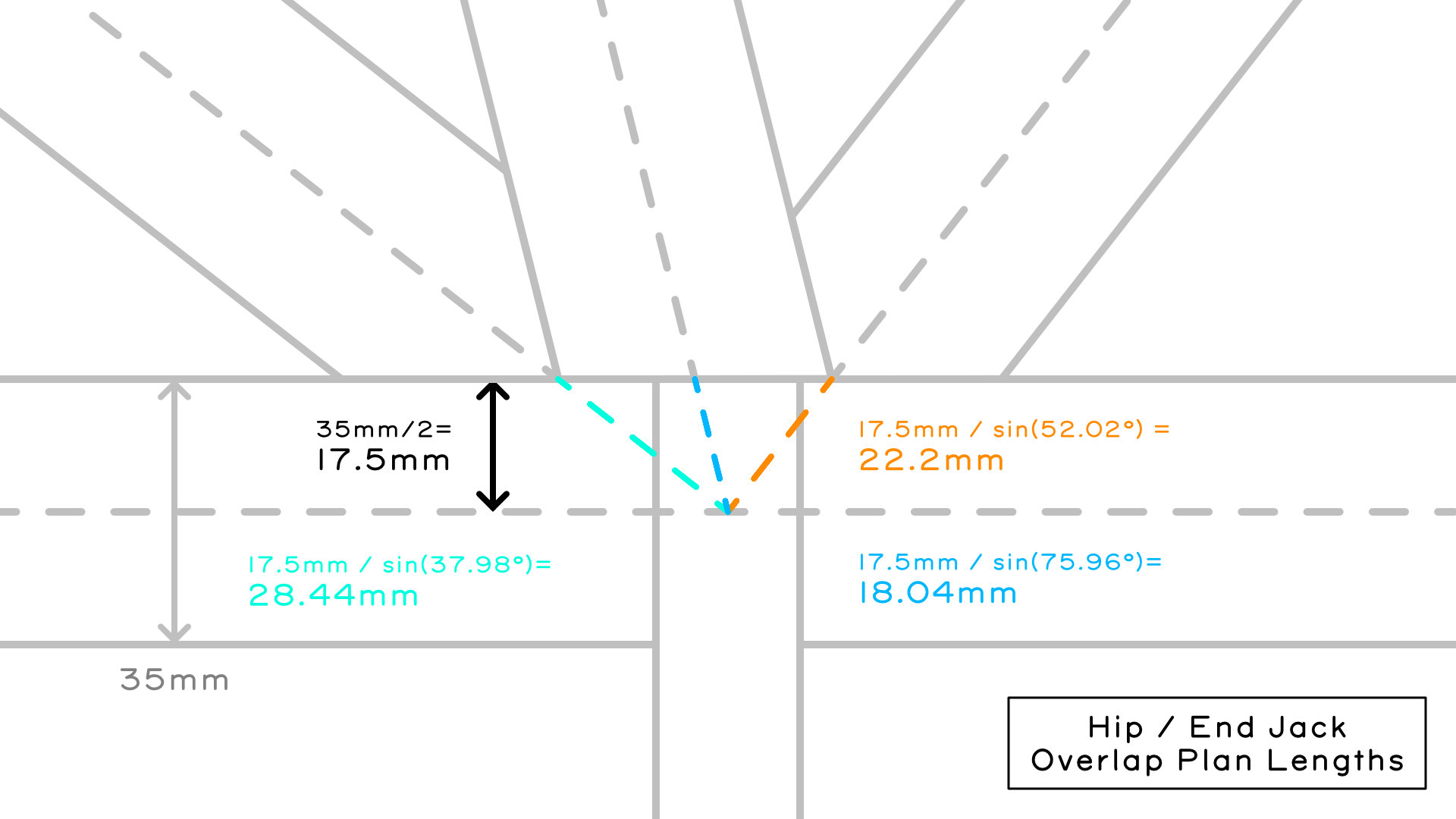
- One last step before cutting the lengths is to recognise that the meeting point of these lengths is a gathering point at the end of the ridgeboard, aligned midway to the rafters and hips. Our calculated lengths have overlaps that need to be deducted. The process is very similar to what we have done to calculate the lengths. To begin calculating the overlaps we find the plan length of the overlaps. To do this, we use half of the rafter thickness, and the plan angles of the end jack and hips from the gathering point. The plan lengths have their respective pitches applied to get their actual lengths. The diagrams illustrate this below. The overall formula is: overlap length = (half rafter thickness / sin(plan angle from gathering point)) / cos(pitch), nb. if the plan angle is from the hip side, substitue 'sin(plan angle from gathering point)' for 'cos(plan angle from hip)'
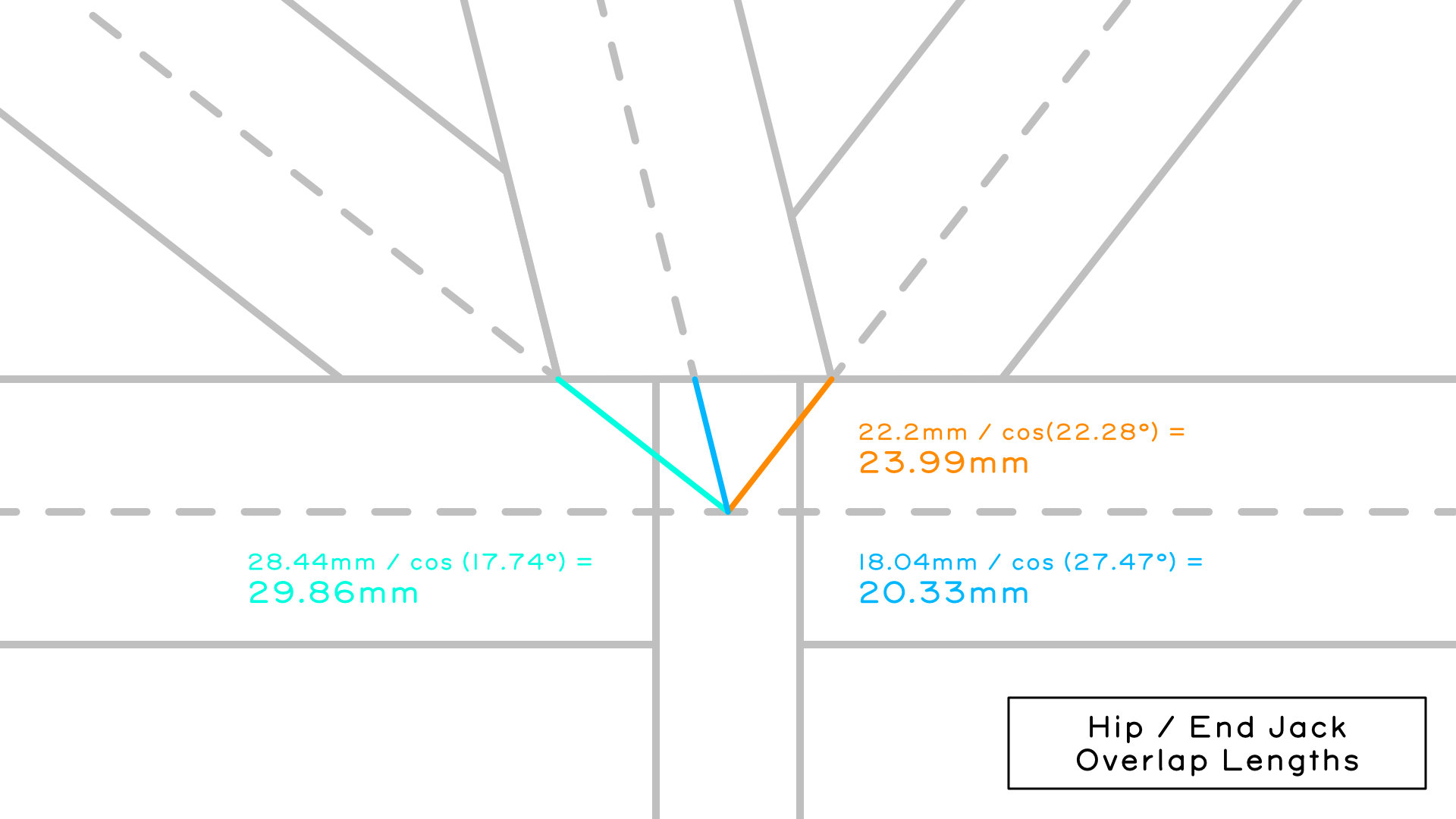
- Short Hip Overlap: (17.5mm / sin(37.98°)) / cos (17.74°) OR (17.5mm / cos(52.02°)) / cos (17.74°) = 29.86mm
- End Jack Overlap: (17.5mm / sin(75.96°)) / cos (27.47°) = 20.33mm
- Long Hip Overlap: (17.5mm / sin(52.02°)) / cos(22.28°) OR (17.5mm / cos(37.98°)) / cos(22.28°) = 23.99mm
Hip Angle Formula
The formula arctan(tan(roof pitch) × sin(hip plan angle)) helps us determine our hip angles, and results from imagining a half-span equal to 1. When we use a half-span of 1, we also know the plan length of the end jack is equal to 1. The plan length of the end jack forms the opposite side of the triangle connected to the hip plan angle, whose hypotenuse is the hip plan length and is equal to: (end jack plan length) / sin(hip plan angle), or 1 / sin(hip plan angle). To get the hip angle, we know our gathering point height for a half-span of 1 is: tan(roof pitch) / 1. The hip angle triangle to solve is formed by the hip plan length and the gathering point height. This triangle is tan(hip angle) = tan(roof pitch) / (1 / sin(hip plan angle)), which we simplify to: hip angle = arctan(tan(roof pitch) × sin(hip plan angle)) 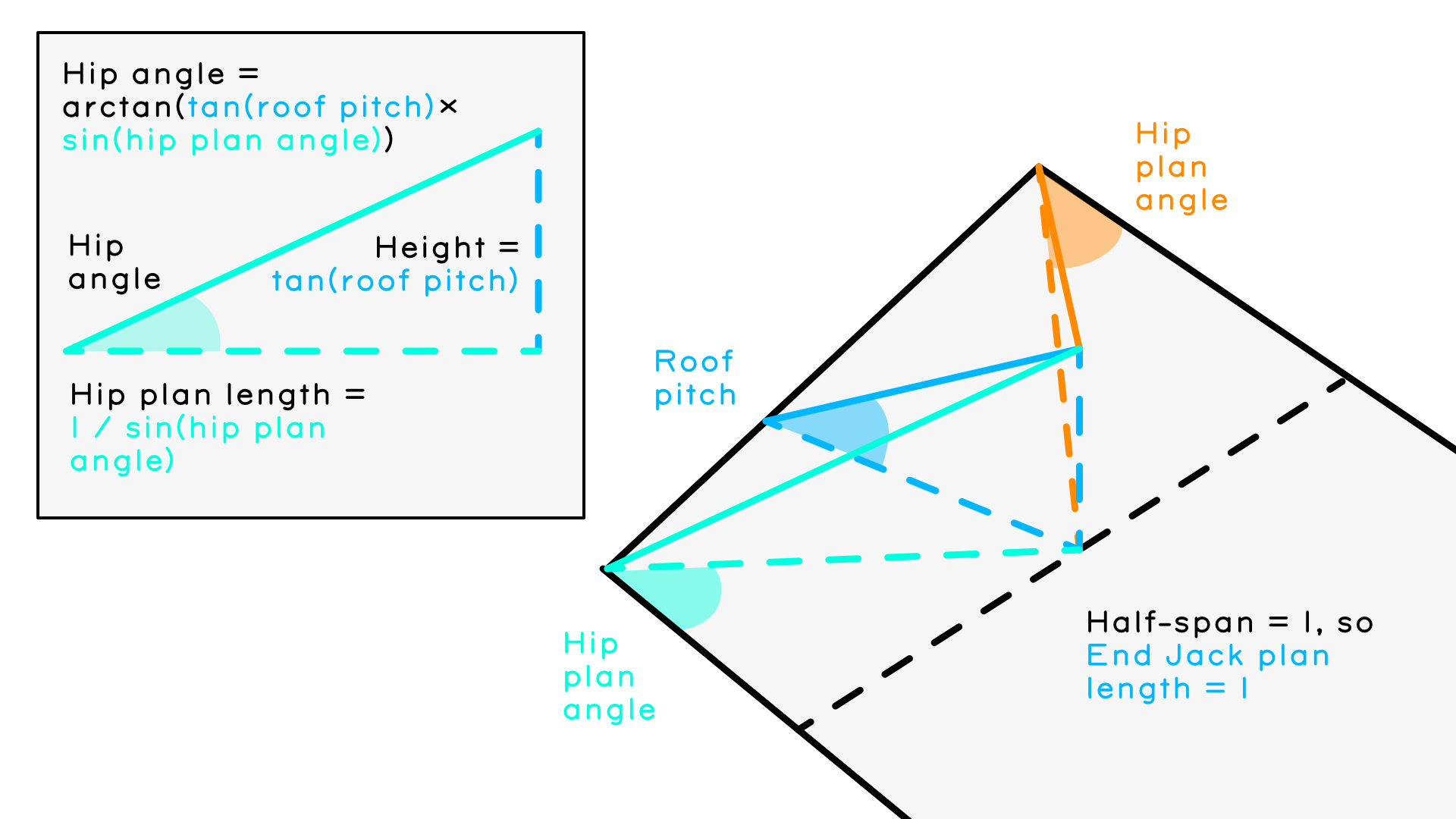
Acknowledgements
I thank Brandon Sarich and Troy Fitzpatrick for teaching me how to build oblique hip roofs at TIV. Brandon’s help in validating the calculations refined the hip angle formula, and Troy’s enthusiasm for my initial plan angle calculations inspired me to make this guide.